
When designing a study for causal mediation analysis, it is crucial to conduct a power analysis to determine the sample size required to detect the causal mediation effects with sufficient power. However, the development of power analysis methods for causal mediation analysis has lagged far behind. To fill the knowledge gap, I proposed a simulation-based method and an easy-to-use web application (https://xuqin.shinyapps.io/CausalMediationPowerAnalysis/) for power and sample size calculations for regression-based causal mediation analysis. By repeatedly drawing samples of a specific size from a population predefined with hypothesized models and parameter values, the method calculates the power to detect a causal mediation effect based on the proportion of the replications with a significant test result. The Monte Carlo confidence interval method is used for testing so that the sampling distributions of causal effect estimates are allowed to be asymmetric, and the power analysis runs faster than if the bootstrapping method is adopted. This also guarantees that the proposed power analysis tool is compatible with the widely used R package for causal mediation analysis, mediation , which is built upon the same estimation and inference method. In addition, users can determine the sample size required for achieving sufficient power based on power values calculated from a range of sample sizes. The method is applicable to a randomized or nonrandomized treatment, a mediator, and an outcome that can be either binary or continuous. I also provided sample size suggestions under various scenarios and a detailed guideline of app implementation to facilitate study designs.
Avoid common mistakes on your manuscript.
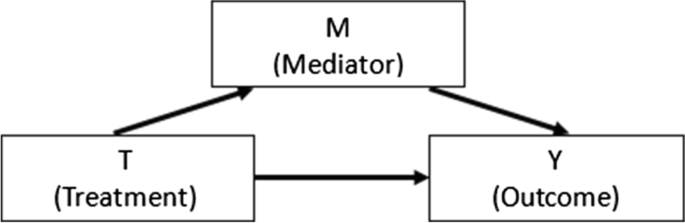
Mediation analyses are widely employed for investigating the mediation mechanism through which a treatment achieves its effect on an outcome. In the basic mediation framework, as shown in Fig. 1, a treatment affects a focal mediator, which in turn affects an outcome. For example, a researcher aims to evaluate the impact of a growth mindset by randomly assigning students to an intervention group that conceptualizes intelligence as malleable and a control group that only focuses on brain functions while not emphasizing intelligence beliefs. In theory, the treatment T may enhance students’ challenge-seeking behaviors M, which may subsequently promote their academic outcomes Y. Hence, the researcher plans to further examine the hypothesized mechanism by decomposing the total treatment effect into an indirect effect transmitted through challenge-seeking behaviors and a direct effect that works through other mechanisms.
Path analysis and structural equation modeling (SEM) (e.g., Baron & Kenny, 1986) that rely on a regression of the mediator on the treatment, and a regression of the outcome on the treatment and the mediator, have been adopted as primary approaches for mediation analysis. However, they usually overlook a possible treatment-by-mediator interaction. For example, challenge-seeking behaviors may generate a higher impact on academic outcomes under the growth mindset intervention condition than under the control condition. Ignoring the interaction would lead to biased indirect and direct effect estimates. Besides, they pay little attention to confounders of the treatment–mediator, treatment–outcome, and mediator–outcome relationships. Although the first two relationships are unconfounded when the treatment is randomized, the third one is usually confounded because mediator values are often nonrandomized. For instance, a student who had a higher grade point average (GPA) before the treatment may be more likely to seek challenges and have higher academic achievement in the long run. Therefore, baseline GPA may confound the relationship between challenge-seeking behaviors and academic outcomes. Omitting a confounder from the analysis would bias the indirect and direct effect estimates.
A natural question that a researcher would raise when designing a study for investigating mediation mechanisms is, “How many observations should I collect to achieve an adequate power for detecting an indirect effect and/or a direct effect based on my chosen mediation analysis method?” Power analysis is an important step of study design for determining the sample size required to detect effects with sufficient power, which is the probability of rejecting a false null hypothesis. Almost all the existing power analysis strategies for mediation analysis have been developed based on the traditional SEM framework ignoring the treatment-by-mediator interaction and confounding bias. While a few derived power formulas (e.g., Vittinghoff et al., 2009), most were developed based on Monte Carlo simulations that repeatedly draw samples of a specific size from a defined population and calculate power as the proportion of the replications with a significant result (e.g., Fossum & Montoya, 2023; Fritz & MacKinnon, 2007; Muthén & Muthén, 2002; Schoemann et al., 2017; Thoemmes et al., 2010; Zhang, 2014). The simulation-based approach is more widely used because it is intuitive and flexible and may be the only viable method when models are complex (VanderWeele, 2020) or the normality assumptions of data and effect estimates are violated (Zhang, 2014).
Nevertheless, power analysis for causal mediation analysis remains underdeveloped. To the best of my knowledge, Rudolph et al. (2020) is the only study that assessed the power of single-level causal mediation analysis methods. They compared through simulations the power of regression-based estimation, weighting-based estimation, and targeted maximum likelihood estimation, which is a doubly robust maximum-likelihood-based approach. While they introduced a simulation-based procedure for power calculation, they did not develop statistical software for easy implementations, nor did they offer a way to calculate the sample size for achieving a given power, which is essential for study design. In addition, they focused on a binary mediator and a binary outcome while not considering other common scales. Moreover, they fitted linear probability models to binary mediator and outcome, which is problematic when covariates are continuous (Aldrich & Nelson, 1984).
VanderWeele (2020) suggested that it is urgent to develop easy-to-use power analysis tools for causal mediation analysis. To fill the knowledge gap, I developed a simulation-based power analysis method and a user-friendly web application for sample size and power calculations for a causal mediation analysis with a randomized or nonrandomized treatment, a mediator, and an outcome that can be either binary or continuous. I also provided tables of sample sizes needed to achieve a power of 0.8 (which is conventionally considered adequate [Cohen, 1990]) for detecting indirect and direct effects under various scenarios, which can be used as guidelines for causal mediation analysis study designs. Different causal mediation analysis methods vary in the degree of reliance on correct model specifications and thus have different power values under different scenarios. Given that regression-based methods are most commonly used in real applications (Vo et al., 2020), I focused on developing a power analysis tool for the regression-based methods that adjust for the treatment-by-mediator interaction and confounders. In addition, I used the Monte Carlo confidence interval method for testing, because it allows the sampling distributions of causal effect estimates to be asymmetric and is less computationally intensive than the bootstrapping method. Because the regression-based methods are more efficient than the weighting- and imputation-based methods, larger sample sizes are expected for the weighting- or imputation-based method to achieve an adequate power than the regression-based methods if the mediator and outcome models are correctly specified.
This article is organized as follows. I first briefly introduce the definition and identification of mediation effects under the counterfactual causal framework, considering both binary and continuous mediator and outcome. I then introduce the estimation and inference method that the proposed power analysis tool relies on. After delineating the simulation-based power analysis procedure, I provide guidelines for researchers to determine how many observations need to be collected for achieving adequate power under various scenarios. I then illustrate the use of the web application for implementing the proposed approach. Finally, I discuss the strengths and limitations of the method, as well as future directions.
Under the counterfactual causal framework, which is also known as the potential outcomes framework, we can define the causal mediation effects for each individual by contrasting their potential outcomes without relying on a particular statistical model. In the growth mindset example introduced earlier, individual i’s treatment T = 1 if assigned to the growth mindset intervention group and T = 0 if assigned to the control group. The individual has two potential mediators, i.e., potential challenge-seeking behaviors. One is under the growth mindset intervention condition, Mi(1), and the other is under the control condition, Mi(0). Similarly, the individual has two potential outcomes, i.e., potential academic outcomes, Yi(1) and Yi(0). Mi(t) and Yi(t) are observed only if the individual was assigned to T = t, where t = 0, 1. In the mediation framework, as represented by Fig. 1, Y is affected by both T and M. Under the composition assumption, the potential outcome Yi(t) can be alternatively expressed as a function of the treatment and the potential mediator under the same treatment condition, i.e., Yi(t, Mi(t)) (VanderWeele & Vansteelandt, 2009). The definitions of the potential mediator and potential outcome rely on the stable unit treatment value assumption (SUTVA) (Rubin, 1980, 1986, 1990): (1) only one version of each treatment condition, (2) no interference among individuals, and (3) consistency. The consistency assumption is that, among the individuals whose T = t, the observed mediator takes the value of M(t), and among the individuals whose T = t and M = m, the observed outcome takes the value of Y(t, m) (VanderWeele & Vansteelandt, 2009).
A contrast of the potential outcomes under the two treatment conditions defines the total treatment effect for individual i, TEi = Yi(1, Mi(1)) − Yi(0, Mi(0)). To further decompose the total effect into an indirect effect and a direct effect, we need to introduce two additional potential outcomes that are never observable: Yi(1, Mi(0)), individual i’s potential academic outcome if the treatment is at the growth mindset intervention condition while his or her potential challenge-seeking behaviors take the value that would be observed under the control condition, and its opposite Yi(0, Mi(1)). Hence, the total treatment effect can be decomposed into the sum of the total indirect effect TIEi = Yi(1, Mi(1)) − Yi(1, Mi(0)) Footnote 1 and the pure direct effect PDEi = Yi(1, Mi(0)) − Yi(0, Mi(0)), or the sum of the pure indirect effect PIEi = Yi(0, Mi(1)) − Yi(0, Mi(0)) and the total direct effect TDEi = Yi(1, Mi(1)) − Yi(0, Mi(1)) (Robins & Greenland, 1992). TIE and PDE were respectively called as natural indirect effect and natural direct effect by Pearl (2001). I used the terms TIE and PDE here to better contrast with TDE and PIE. The two decompositions are equivalent if the treatment does not affect the mediator when affecting the outcome. A discrepancy between TIEi and PIEi, or equivalently a discrepancy between TDEi and PDEi, indicates a natural treatment-by-mediator interaction effect, INTi = TIEi − PIEi = TDEi − PDEi.
If the treatment T has more than two categories or is continuous, 1 and 0 in the above definitions can be replaced with any two different values of T, t and t ′ (Imai et al., 2010a; VanderWeele & Vansteelandt, 2009). By taking an average of each effect over all the individuals, we can define the population average effects as listed in Table 1. The whole set of TIE, PDE, PIE, TDE, and INT is referred to as causal mediation effects throughout this article, because the mediation mechanism is revealed by all these effects as a whole.
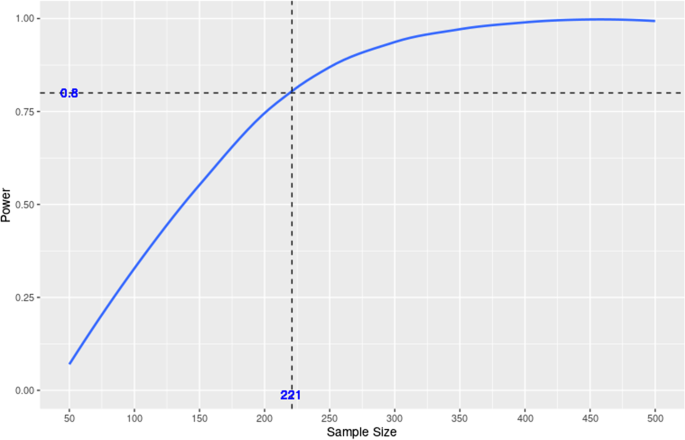
In the power curve, dashed lines are added to mark the target power and the corresponding sample size. The table below lists all the sample sizes used for generating the curve and the corresponding power values. The target power and the corresponding sample size are also included and indicated in bold. For example, Fig. 2 and Table 7 indicate that the sample size needed for detecting a total indirect effect with a power of 0.8 under the default setting is approximately 221. If the objective is to calculate power at a target sample size, dashed lines that mark the target sample size and the corresponding power value will be added to the power curve instead, and the target sample size and the corresponding power value will be included in the table instead. Before a new run, please make sure to click the “Clear” button at the bottom of the output on the right panel.
It takes 49 seconds to run the default setting in which both the mediator and outcome are continuous. If the mediator is continuous and the outcome is binary, or if the mediator is binary and the outcome is continuous, it will take 9 minutes. If both the mediator and outcome are binary, it will take 15 minutes. When either the mediator or the outcome is binary, users may (1) save time by specifying a large sample size range with a large step size and a small number of replications (e.g., 100) in a preliminary assessment and (2) then specify a narrower sample size range with a smaller step size and increase the number of replications in the final run to improve the precision and stability of the results.
While the existing literature of power analysis for causal mediation analysis is almost blank, this study filled the knowledge gap by developing a simulation-based power analysis method for regression-based causal mediation analysis, as well as a user-friendly web application. The first step is to define a population with hypothesized models and parameter values, from which samples of a specific size are repeatedly generated. The second step is to fit the hypothesized mediator and outcome models to each sample, and estimate and test a causal mediation effect at a given significance level using the Monte Carlo confidence interval method. The third step is to calculate the power as the percentage of samples with a significant result. Users can also calculate the sample size required for achieving a specific power based on power values calculated from a range of sample sizes. The method is applicable to binary or continuous treatment, mediator, and outcome in randomized or observational studies. It is intuitive, flexible, and easy to implement. In addition, it does not require the causal effect estimates to be normal.
It is worth noting that the proposed power analysis approach is only applicable to regression-based causal mediation analysis with the Monte Carlo confidence interval method for estimation and inference. In other words, if researchers adopt the proposed method for power analysis at the design stage, they should use the regression-based causal mediation analysis method and estimate and test the causal mediation effects with the Monte Carlo confidence interval method at the analysis stage. The analysis can be conducted using the R package mediation . Since the regression-based approach is more efficient than the other causal mediation analysis methods such as the weighting-based or imputation-based method when the mediator and outcome models are correctly specified, the proposed approach may provide users with guidelines on the minimum number of observations they should collect to achieve a specific power or the maximum power they can achieve at a specific sample size. To calculate the exact power or sample size for the other causal mediation analysis methods, researchers may simply extend the proposed power analysis procedure by implementing the other causal mediation analysis methods in Step 2 (estimation and inference).
An important and challenging component of a power analysis is the specification of the parameter values. Some may specify the parameters based on normative criteria or external constraints. Others may use parameter estimates from previous studies or pilot studies. There is no concern about the former, but the latter is criticized due to the uncertainty of the parameter estimates, which could result in underpowered studies (Liu & Wang, 2019), and the problem is particularly severe if the sample sizes of the previous studies or pilot studies are small (Liu & Yamamoto, 2020). Liu and Wang (2019) developed a power analysis method that considers uncertainty in parameter estimates for traditional mediation analysis. They modeled the uncertainty in the parameter estimates via their joint sampling distribution and calculated a power value based on each random draw of parameter estimates from their sampling distribution. Hence, instead of producing one single power value, they provided a power distribution at a specific sample size. The idea can be extended to power analysis for causal mediation analysis.
Several other extensions can be incorporated into the web application in the future.
First, the current study allows treatment, mediator, and outcome to be binary, normal, or nonnormal with nonzero skewness and kurtosis. The proposed procedure can be further extended for applications to categorical data with more than two categories, count data, and survival data.
Second, in this study, the treatment–mediator, treatment–outcome, and mediator–outcome relationships, as well as the relationship between the treatment-by-mediator interaction and the outcome, are assumed to be constant. However, in many applications, the relationships may vary by different individuals or contexts, and it is of interest to investigate the heterogeneity of mediation mechanisms. Hence, a causal moderated mediation analysis is needed. Qin and Wang (2023) developed an R package moderate.mediation for easy implementations of regression-based causal moderated mediation analysis with the Monte Carlo confidence interval method for estimation and inference. A compatible power analysis tool will be further developed by incorporating moderators in the population models in Step 1 (data generation) and the analytic models in Step 2 (estimation and inference).
Third, this study assumes no posttreatment confounding of the mediator–outcome relationship. In other words, the relationship between the mediator and outcome is not confounded by any variables that are affected by the treatment. However, such confounders may exist in many real applications. For example, in the growth mindset example, students in the intervention group may engage more with the treatment messages and thus be more motivated for challenge seeking and have a higher GPA. Therefore, treatment engagement is a potential posttreatment confounder of the relationship between challenge-seeking behaviors (mediator) and academic performance (outcome). Some researchers have developed sensitivity analysis strategies to assess the influence of posttreatment confounding (Daniel et al., 2015; Hong et al., 2023). Others have developed causal mediation analysis from the interventional perspective that allows for posttreatment confounding (e.g., VanderWeele et al., 2014). Despite the limitations of Rudolph et al. (2020), as explicated in the introduction section, they considered posttreatment confounding in power analysis for causal mediation analysis from the interventional perspective. However, they focused on binary mediator and outcome and used linear probability models that may be problematic when covariates are continuous. Extensions can be made to the proposed procedure in the current study by updating the population models in Step 1 (data generation) and the analytic models in Step 2 (estimation and inference) under the framework that can accommodate posttreatment confounders.
Fourth, power analysis for mediation analysis in multilevel designs has not been discussed until recently. Kelcey et al. (2017a, 2017b) derived power for indirect effects in group-randomized trials. They focused on a randomized and binary treatment, a normal mediator, and a normal outcome. Group-randomized trials randomize treatments at the group or site level and thus do not allow for investigating between-site heterogeneity. More and more multi-site trials have been designed for assessing between-site heterogeneity of treatment effects. To better understand why a treatment effect varies across sites, it is crucial to further investigate the heterogeneity of the underlying mechanisms via multi-site causal mediation analysis (Qin & Hong, 2017; Qin et al., 2019; Qin et al., 2021a). However, no power analysis tools have been developed for this line of research. The proposed power analysis tool can be extended by replacing the single-level models in Steps 1 and 2 with multilevel models for researchers to determine the sample size per site and number of sites required for such studies.
Fifth, additional extensions can be made for power analysis for causal mediation analysis that involves multiple mediators, power analysis for longitudinal mediation analysis, and power analysis that incorporates missing data or measurement error.
Sixth, in addition to the power of detecting an effect, there could be other targets of sample size planning, such as the accuracy in parameter estimation (e.g., Kelley & Maxwell, 2003) and the strength of evidence for competing hypotheses based on Bayes factors (e.g., Schönbrodt & Wagenmakers, 2018). Extensions can be made to develop sample size planning methods for causal mediation analyses that aim at these alternative targets.